霍金在《大设计》中曾用生命游戏来举例,说明简单定律可能产生智慧生命拥有的复杂特征。因为生命游戏中会出现一些自复制的样式,这让人想到生命进化的基本机制。然而用计算机演算发现一个随机化生成的256*256的方格世界在大约5000步左右就会到达僵死状态,中间出现的有趣现象很有限(适当定义“熵”,生命游戏中也存在熵增定律)。
不过如果把生命游戏类比于真实的物理世界,生命游戏里的单元格仅相当于普朗克长度,而时间演化的一步相当于普朗克时间,很有可能要出现复杂的自组织现象需要相当庞大的格子数量(考虑1米=0.6*10^35普朗克长度),并演化相当长的时间(考虑1秒=0.2*10^44普朗克时间)。
假如真的模拟一个超级庞大的方格,很有可能只要随机初始化这个世界,秩序就会从混沌中涌现,简单的物理规则组合出复杂的化学现象,然后在一个很大的尺度上可能会出现类似DNA的带有遗传密码的可以遗传变异的类生命现象,这种生命最终演化出智能和自我意识。他们会想些什么呢?
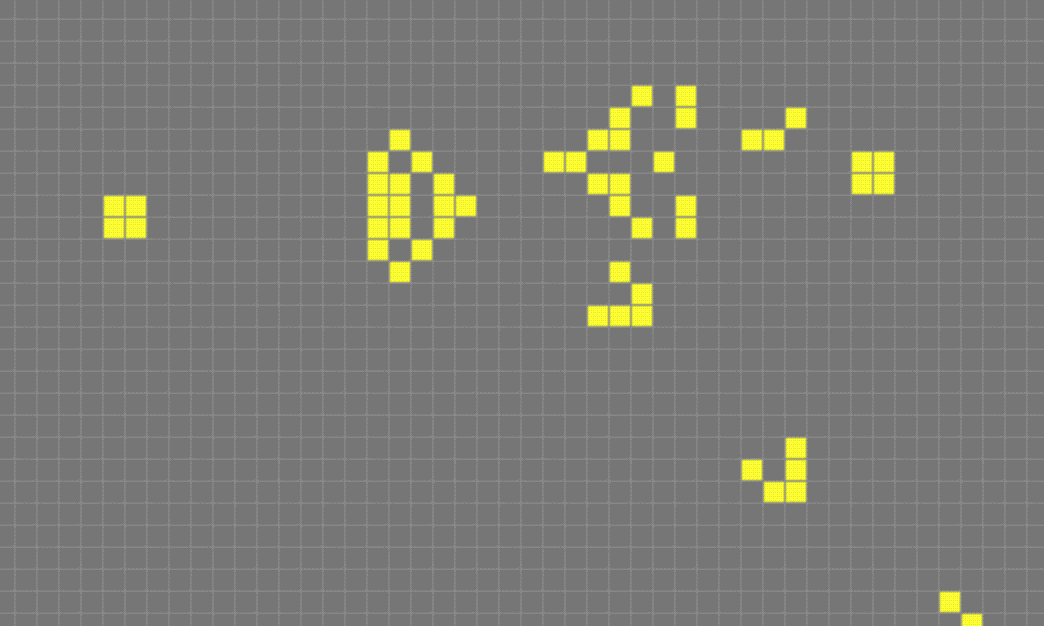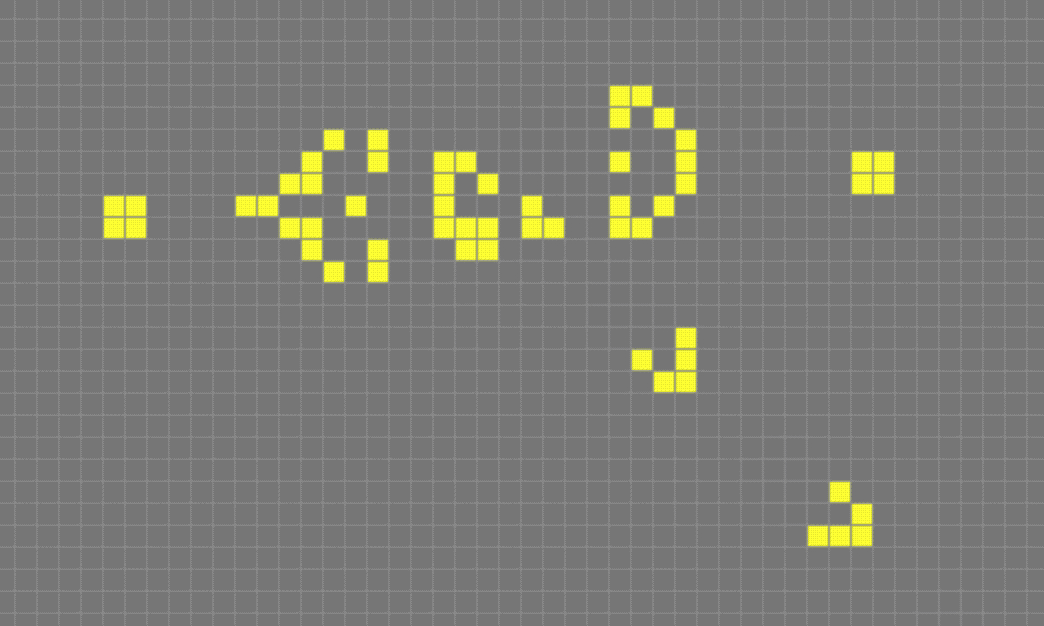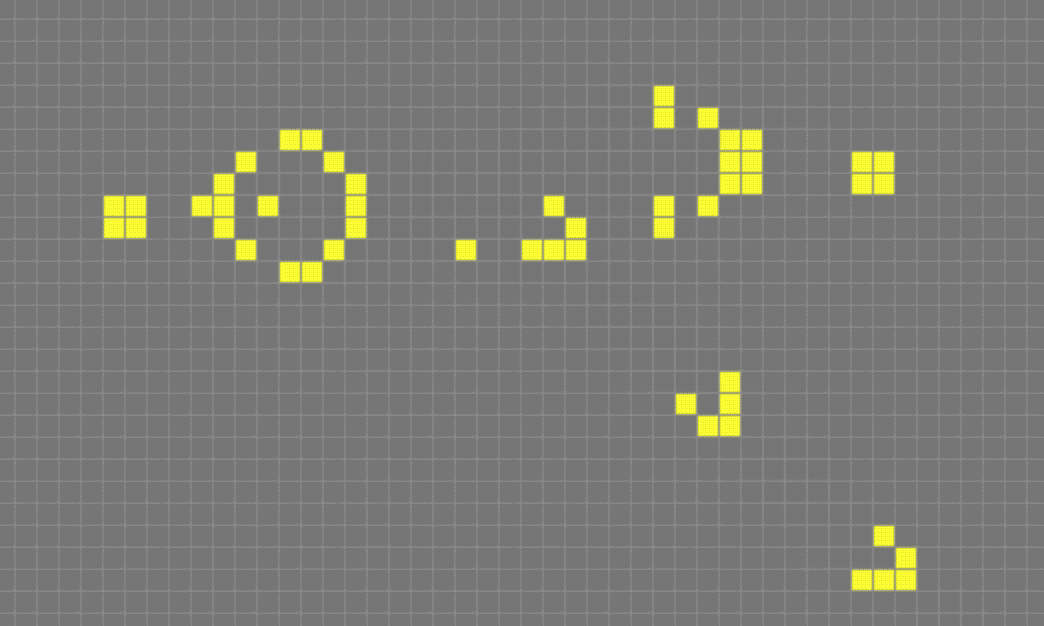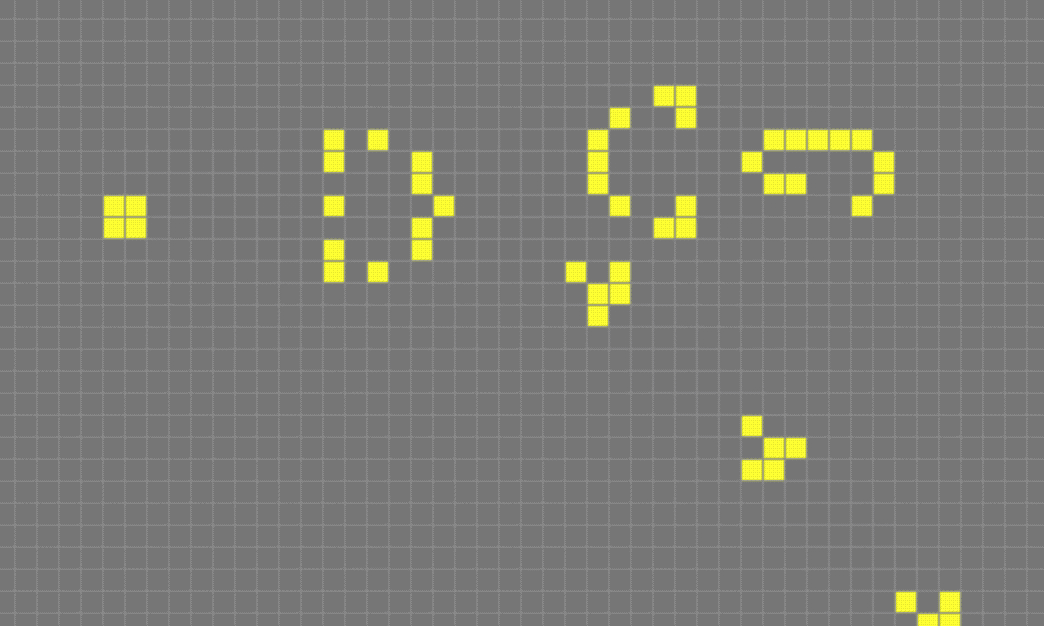
什么是康威生命游戏?
康威生命游戏(Conway\'s Game of Life),又称康威生命棋,是最著名的二维元胞自动机,由英国数学家约翰·康威(John H. Conway)发明,1970年10月,通过马丁·加德纳(Martin Gardner)在《科学美国人》开设的专栏中得到普及。游戏像“病毒”一样在世界范围内传播。
尽管这个游戏中的规则是完全确定的,但是很难预测几个步骤后的状态。简单来说,该游戏是零玩家游戏,这意味着我们只能设定其初始状态,并观察其演变,它的发展由其初始状态决定。
它是具有图灵完整性的,可以模拟通用构造器或任何其他图灵机。也就是从理论上来说单元格空间足够大、数量足够多、计算能力足够强,生命游戏甚至可以模拟出与和真实生命程度相当的复杂性。
康威生命游戏(Game of Life)没有游戏玩家各方之间的竞争,也谈不上输赢,可以把它归类为仿真游戏。事实上,也是因为它模拟和显示的图像看起来颇似生命的出生和繁衍过程而得名为“生命游戏”。在游戏进行中,杂乱无序的细胞会逐渐演化出各种精致、有形的结构;这些结构往往有很好的对称性,而且每一代都在变化形状。一些形状一经锁定就不会逐代变化。有时,一些已经成形的结构会因为一些无序细胞的“入侵”而被破坏。但是形状和秩序经常能从杂乱中产生出来。
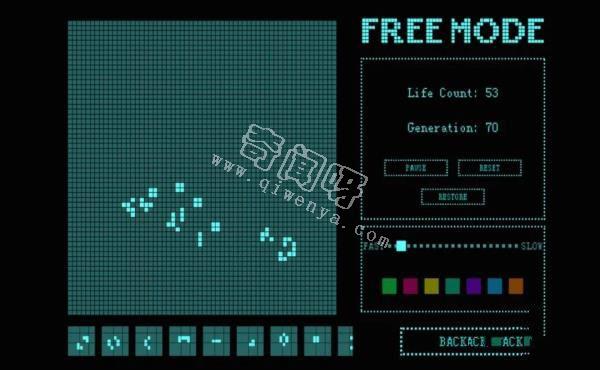
生命游戏的规则
我们所说的生命游戏是一个无限的,由二维正交正方形的网格组成的计算机模拟图像。每个单元可能出现两种状态:活或死的(填充或未填充的分别)。每个单元格都与其八个相邻的单元交互,这八个单元格是水平、垂直或对角线相邻的单元格。在每个时间步上,都会发生以下变化:

当前元胞为存活状态时,如果周围的存活元胞数小于2或大于3,该元胞变成死亡状态。
当前元胞为存活状态时,如果周围有2个或3个存活元胞时,该元胞保持原样。
当前元胞为死亡状态时,如果周围有3个存活元胞时,该元胞变成存活状态。
可以把最初的元胞结构定义为种子,当所有在种子中的元胞同时被以上规则处理后,可以得到第一代元胞图。按规则继续处理当前的元胞图,可以得到下一代的元胞图,周而复始。
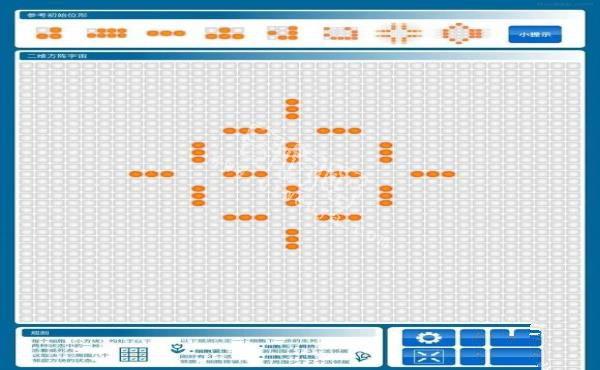
Matlab上很容易实现生命游戏的仿真。例如在一个50乘以50的“矩阵宇宙”中,我把自己的名字作为初始群体,然后发现进化65代以后,“宇宙”中就没有“生命”迹象了……
现在,假设我很喜欢一个女生,然后我把我们的名字分别写在“宇宙”的左上角与右下角,如果发现两个群体在足够长的进化过程中始终没法产生交集(当然这里需要更细致地定义)。那么,这是不是意味着现实中两个人会很难走到一起呢?
只有玩过这个游戏才知道,世界是这个样子太不容易了,无数中可能中只有一种可能才能趋于完美,其余可能几乎都是没有生命。

生命游戏的应用
自从发明以来,康威的《生命游戏》就吸引了人们的极大兴趣,这是因为自动机的状态发展令人惊讶。生命游戏是产生并自我组织的一个例子。计算机科学,物理学,生物学,生物化学,经济学,数学,哲学和生成科学等各个领域的学者都可以用这种通过执行简单规则即可产生复杂模式的方式。
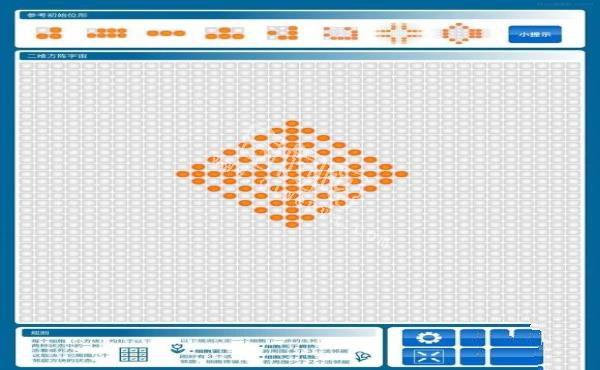
生命游戏也可以用作教学分析,用于展现有些反直觉的观念,即设计和组织可以在没有设计师的情况下自发出现。例如,认知科学家丹尼尔·丹内特(Daniel Dennett)广泛使用了康威生命游戏中的 “宇宙” 的类比,来说明复杂的哲学构造(如意识和自由意志)可能从相对简单的确定性物理定律集演化而来,而这些定律可以控制我们的宇宙。